Binary numbers, logic gates, binary Encryption

Encryption Project: XOR Stream Cipher (Binary Intro)

In this project I will be guiding you (the reader) through the process of making a secure binary encryption. To some binary numbers may seem shrouded in mystery and secrecy, a classified code that only natural born geniuses can understand. However, binary numbers can be boiled to two simple values that even someone with zero knowledge of computer hardware and software can understand.

What are Binary Numbers?

So what is a Binary Number? Well, as I’m sure you’ve seen before, or guessed by the bi prefix, Binary consists of a 1 or 0, but what does that really mean? A computer, at the most basic level contains a series of on and off switches. 1 representing on and 0 representing off. You could go a step further and assign binary numbers to a boolean value True(1) or False(0). Now lets convert a Binary number to our number system. Unlike the base 10 system Binary uses the base 2 system

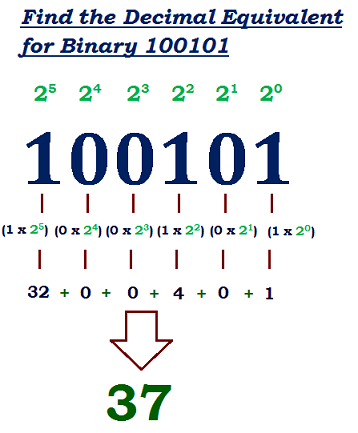
Bits and Bytes

Now that you understand that Binary isn’t dark magic, lets look into the grouping of Binary. To keep it short, a bit is a single binary digit, 8 bits makeup a byte. A word on your computer screen is usually 32 bits or 4 bytes of data. Bytes can store data and execute basic instructions. You’ve probably heard byte before when shopping for electronics, kilobyte, megabyte, gigabyte, terabyte, etc etc.. A kilobyte is 1024 bytes, a megabyte is 1024 kilobytes and a gigabyte 1024 megabytes, you get the point. Now that we’ve built a solid foundation in Binary lets make the encryption!

Logic Gates

OK ok, I know I said we would begin on encryption, but understanding logic gates is kind of crucial if you want to write the encryption. Remember earlier when I assigned binary numbers to a Boolean value? Well, that will come in handy now. Just like an if statement in Python, logic gates use Boolean Values. The following are common Boolean operators:

• AND, checks if both statements are True
• OR, checks if at least one of the statements are True
• NOT, changes the Boolean values of a statement, true to false or false to true The term “logic gate” originates from how electronic circuits handle Booleans, on(true) off(false).

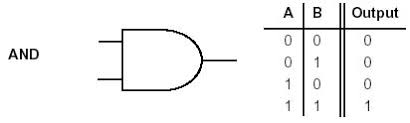
  And Gates

  And gates take in two bits as an input and produce a single bit as an output. If both input bits are a 1(true) then the output bit is a 1(true). Just like the And operator used in regular Python if both conditions are True the output is True, if one of the conditions in false the output is False. On paper an And logic gate is often written in a D.

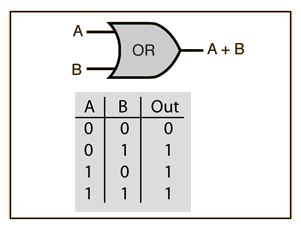
  Or Gates

  Or gates, just like And gates take in two bits as an input and produce 1 bit as an output. I like to think of an Or gate as the opposite of an And gate. In an Or gate if any inputs are a 1(true) then the output will be 1(true), but if both inputs are 0(false) then the output with be 0(false). On paper:

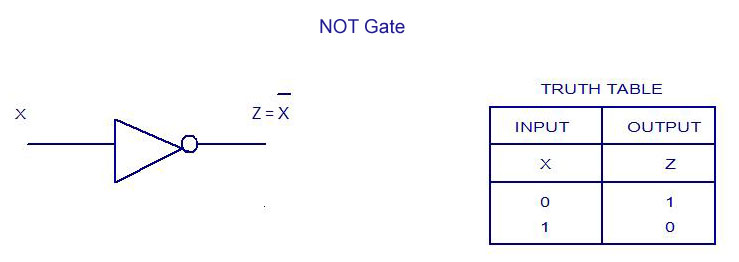
  Not Gates

  Unlike the others the Not gate only takes in one input and produces one output. Out of all the Logic gates this one is my favorite because of it’s simplicity. It takes in one bit and the output is the inverse bit. For example, if you passed in a 1(true) the output would be 0(false). On paper:

  Using Logic Gates in Python

  Now we will see how these logic gates work in a Python IDE

  1. Create two variables with different binary numbers using binary notation (0b)

       A = 0b1110
       B = 0b0101
     

  2. Use bit-wise operators that take in the two binary numbers(except for the Not gate use one variable) as inputs (& = And gate, | = Or gate, ~ = Not gate)

       A = 0b1110
       B = 0b0101
       X = A & B
       Y = A | B
       Z = ~A
     

  3. Use the built in bin() function to print the outputs

       A = 0b1110
       B = 0b0101
       X = A & B
       Y = A | B
       Z = ~A
       print(bin(X))
       print(bin(Y))
       print(bin(Z))
     

     If you used the same variables as me you should get the outputs

     0b100
     0b1111
     -0b1111
     

     Z’s output?

     You may have noticed you got a negative Binary number. Python treats the Not operator as using the equation:-(x + 1). Since Math can get a little wacky in binary, we use a few different ways to deal with negative numbers. I won’t be going into great detail on all these methods for the sake of brevity, so I’ll link to a good video that explains it better than I could. The most important methods to remember are sign bits, the one’s complement, and the two’s complement. The equation above simulates the two’s complement where negative values represent a value subtracted by 2 raised to the number of bits. Luckily we won’t be dealing with the Not logic gate for this project.

XOR Logic Gate

The exclusive or gate or XOR gate, like many other gates, takes in two inputs. However, the XOR gate only produces a 1 bit when the inputs are contrary. For example a 1 and 0 input would give an output of 1 while an input of 1, 1 or 0, 0 would produce an output of 0. The XOR gate is useful for encrypting data because it’s technically made up of three different types of gates.

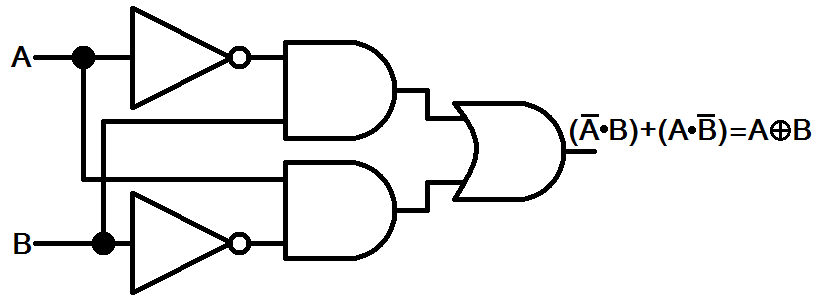
XOR bit wise operator

Just like the other gates XOR also has a bit wise operator which can be used as such:

    #using the variables from the previous program
    F = A ^ B
    print(bin(F))

Bit Shifting

Just like a Shift Cipher or Caeser Cipher you can shift bits to the left or right using a convenient built in operator:

    A = 0b1110
    B = 0b0101
    #left-shift operator
    left_shift = A << 1
    #right-shift operator
    right_shift = A >> 1

As you’ve probably guessed you can change the numbers to the right of the operator to change how many places the bit shifts. Right bit shifting removes the right-most bit. You can alter the number of bits removed by adjusting the numbers to the right of the operator. Left shift adds a 0 to the 2⁰ place. If you printed the left_shift and right_shift variables the output would look like this:

  # A shifted one to the left
  0b11100
  # A shifted  one to the right
  0b111

Using bit operations can make beef up an encryption’s defenses because they can shift and change characters in ways that are nearly impossible for humans to decipher.

Recap:

I know I spent all this time chattering about how we were going to use binary numbers for encryption, but it can be used in many other circumstances. Remember earlier when I said binary is a representation of if electricity is flowing(1) or not(0)? Well, logic gates display how circuits handle these electrical pulses. It’s likely you will run into a few of the logic gates when looking through circuit schematics. With this in mind, binary is like a neat little string that ties the hardware and software of a computer together, learning the fundamentals of Binary will allow you to have a better understanding of any electricity based apparatus.

What’s next?

Finally, now that that’s all over with we can begin on out XOR Stream Cipher. I hope my intro to basic Binary was helpful. As you’ve seen nothing in computer science is magic and you can learn it with the right amount of dedication. To begin on the XOR stream cipher click here or navigate to it via the Programming Projects page.